"Voodoo correlations" o cómo inflar las correlaciones en el estudio del cerebro y conseguir que te publiquen el paper.
El asunto tiene miga y es algo complicado para exponerlo en un simple post, no obstante, voy a resumir algunas de las críticas.
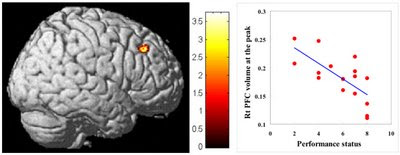
Como muchos lectores de este blog saben, la mayoría de estudios realizados en el campo de la Neurociencia Social tratan de encontrar correlaciones entre medidas de la actividad cerebral, obtenidas mediante técnicas de resonancia magnética funcional (RMNf), y medidas de personalidad o conducta, usualmente obtenidas mediante cuestionarios. Vul señala en su trabajo la sorpresa que le causó observar que muchas de estas correlaciones alcanzaban unos niveles extremadamente altos, en muchos casos por encima de .90.
Como no podría ser de otro modo, tanto las medidas psicométricas como las obtenidas mediante RMNf no ofrecen una fiabilidad perfecta. En el primer caso, es frecuente que los cuestionarios presenten fiabilidades test-retest comprendidas entre .70 y .90, aunque en algunos raros casos pueden ser superiores, y también inferiores. Pero las técnicas de neuroimagen tampoco ofrecen fiabilidades mucho más altas. Aunque pudiera pensarse que la resonancia magnética ofrece fotografías directas del cerebro en acción, no hay que olvidar que se trata de imágenes creadas mediante complejos cálculos estadísticos por un sofisticado software a partir de multitud de datos recogidos. Además, tras la recogida de los datos, los investigadores deben realizar ajustes para corregir desviaciones en función del tamaño cerebral, los movimientos de la cabeza del sujeto o la localización de ciertas estructuras cerebrales, por lo que pueden surgir errores e imprecisiones en todo este proceso (además, complica la detección de errores por parte de los investigadores y de quienes revisan las publicaciones en que se exponen los resultados del estudio).
 Cualquiera que esté algo avezado en estadística sabe que la correlación entre dos medidas no puede ser superior a sus fiabilidades. La razón es evidente: si una medida correlaciona consigo misma .80, es imposible que su correlación con una medida diferente sea más alta. Estaría unos puntos por debajo, incluso en el caso de una asociación casi perfecta entre ambas medidas. Pues bien, ese fue el detalle que le puso a Vul la mosca detrás de la oreja y le llevó a emprender un meta-análisis, tras solicitar a los autores de 55 estudios información acerca de algunos detalles metodológicos que no quedaban claros en los trabajos publicados.
Cualquiera que esté algo avezado en estadística sabe que la correlación entre dos medidas no puede ser superior a sus fiabilidades. La razón es evidente: si una medida correlaciona consigo misma .80, es imposible que su correlación con una medida diferente sea más alta. Estaría unos puntos por debajo, incluso en el caso de una asociación casi perfecta entre ambas medidas. Pues bien, ese fue el detalle que le puso a Vul la mosca detrás de la oreja y le llevó a emprender un meta-análisis, tras solicitar a los autores de 55 estudios información acerca de algunos detalles metodológicos que no quedaban claros en los trabajos publicados.Lo que encontró Vul fue que era bastante usual que los investigadores seleccionasen algunos voxels (como un pixel pero tridimensional que refleja una pequeña área cerebral) que indicaban niveles de actividad en ciertas estructuras cerebrales significativamente distintos de cero, ignorando los demás, y a partir de ellos construían la medida de actividad cerebral. Es como si utilizamos un cuestionario para evaluar la autoestima y relacionarla con el afecto parental, pero en lugar de contar con los 100 ítems que conforman el cuestionario, es decir con la puntuación total en la escala, sólo cogemos aquellos 5 items que muestran las correlaciones más altas con el afecto y usamos su promedio e ignoramos el resto. Seguro que ustedes están pensando que estos neurocientíficos son unos tramposos.
Los investigadores criticados se han defendido argumentando que cierto que seleccionaron grupos de voxels que mostraban correlaciones significativas con la medida psicométrica, pero que, al tratarse de múltiples correlaciones, habían realizado una corrección para determinar el nivel de significación requerido para realizar esa selección. Si no lo he entendido mal se refieren a la corrección de Bonferroni o algo similar. Es decir, en cualquier prueba de significación estadística fijamos un nivel a partir del cual la correlación entre dos variables, o la diferencia observada entre dos medias, es significativa y no se debe al azar. Ese nivel suele ser de .95, lo que quiere decir que en un 5% de ocasiones nos equivocaremos, pues diremos que hay diferencias o asociación significativa entre los valores observados, cuando en realidad no la hay (error alfa o tipo I). Por lo tanto, si se correlacionasen cien voxels, tomados de uno en uno, con una determinada medida psicométrica, por puro azar 5 de esos voxels tendrían correlaciones significativas. Por ello, cuanto más correlaciones hagamos, más exigentes deberemos mostrarnos para considerar que una correlación es significativa, y en lugar del .95 deberemos trabajar con niveles de significación superiores, que pueden llegar a ser de .999, para minimizar la posibilidad de cometer errores alfa. (Volviendo al ejemplo de las escala de autoestima, es evidente que por puro azar 5 items mostrarían correlaciones significativas si trabajamos con un nivel de significación de p= .05).
Pero, como ha argumentado Vul, estas correcciones se hicieron sobre la muestra de voxels seleccionados, no sobre el total de voxels. Este dato es muy relevante, ya que hay que tener en cuenta que estamos hablando de cantidades enormes de voxels, puesto que una sesión normal de RMNf puede producir alrededor de un billón de medidas, que luego se combinan con complejos cálculos. Por lo tanto, aunque la selección parece necesaria, esta selección no aleatoria o sesgada hace que el bloque final de medidas seleccionadas no sea independiente del inicial contribuyendo a inflar las correlaciones (non-independent error).
La pregunta que podemos hacernos es si los autores de los artículos criticados por Vul et al. han cometido algunos errores inocentes o si hay cierta intencionalidad en sus maniobras. ¿Qué interés pueden tener en inflar las correlaciones hasta valores por encima de .08? ¿Por qué no se conforman con algunas correlaciones algo más bajas, aunque igualmente significativas? Pues ahí puede estar el problema, en que es probable que muchas de estas correlaciones dejaran de alcanzar el nivel de significación estadística. Hay que tener en cuenta que los estudios con RMNf son muy costosos y suelen emplear muestras muy reducidas con lo que la potencia estadística de las pruebas es muy baja, y se precisan de correlaciones muy altas para alcanzar el nivel de significación, sobre todo si se aplica una corrección como la de Bonferroni. ¿Qué cara les quedaría a los investigadores si después de tanto gasto y esfuerzo no encuentran lo que están buscando? ¿Quién les publicaría su trabajo? Desde luego ni Science ni Nature.
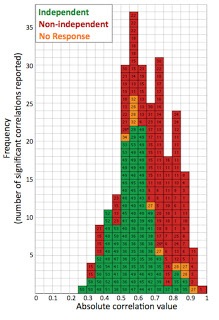
Figura (Vul et al., 2009). El histograma presenta los valores de las correlaciones de los estudios criticados por Vul et al. El color verde representa las provenientes de análisis que no incurrieron en el error de no independencia, evitando por tanto el sesgo de elección de medidas. Los rojos corresponden a los estudios que llevaron acabo análisis no independientes, y que por lo tanto inflaron el valor d elas correlaciones. Los naranjas corresponden a los estudios que no respondieron al cuestionario de Vul. Se observa claramente que los estudios que proporcionan un mayor número de correlaciones significativas elevadas son los que incurrieron en el error de no-independencia.
Algunos otros blogs que han tocado este tema (ver aquí, o aquí, o también aquí)
- Parcial De Tecnicas Psicometricas
Final tomado en diciembre de 2013: 1. ¿Se puede medir en psicología? Explicar los dos modelos y niveles de medición.2. Explicar fuentes de error.3. Luego de leer este artículo, responda las preguntas que se mencionan a continuación:El IAES es una...
- ¿duermen Bastante Nuestros Adolescentes?
Basta con pasarse por la puerta de un instituto a la hora de la entrada para leer en las caras de los adolescentes la falta de sueño que arrastran. Muchos no comienzan a espabilarse hasta bien entrada la mañana, y la mayoría parecen más despiertos...
- Llegan Las Neurociencias
La primera década del presente siglo ha contemplado un avance espectacular en la investigación en neurociencias como consecuencia de la disponibilidad de nuevas y más avanzadas técnicas de neuroimagen. Pero, salvo contadas excepciones, los profesionales...
- The File Drawer Effect O Los Sesgos En Las Publicaciones Científicas
Seguro que quienes os dedicáis a la investigación habéis sentido en más de una ocasión una gran decepción cuándo después de diseñar cuidadosamente una investigación y haber recogido esforzadamente una gran cantidad de datos, los análisis de...
- La Resonancia Magnética Funcional Y El Estudio Del Cerebro En Acción
La verdad es que las técnicas de resonancia magnética funcional (fMRI) producen unas imágenes muy hermosas del cerebro en acción, y está más que justificado el enorme poder de atracción que ejercen sobre muchos investigadores de diversos campos...
